Formule. Sia un tronco di cono d'altezza e le cui basi hanno raggi e .Il volume del tronco è pari a = (+ +). La superficie laterale del tronco di cono è data dalla formula = (+) dove è l'apotema, la lunghezza del lato obliquo del tronco di cono, pari a = + (). La superficie totale del cono è data dalla formula: = +, oppure = + (+). Dimostrazione della formula del volume. La questione posta non è chiara. Per sviluppare il cono sul piano basta tracciare un settore di cerchio il cui raggio R è uguale alla lunghezza L dell'apotema del cono e nel quale la lunghezza della parte curva è uguale alla lunghezza della circonferenza di base del cono, cioè S = 2π r.. Con una semplice proporzione si vede che l'angolo a, che determina il settore di cerchio.

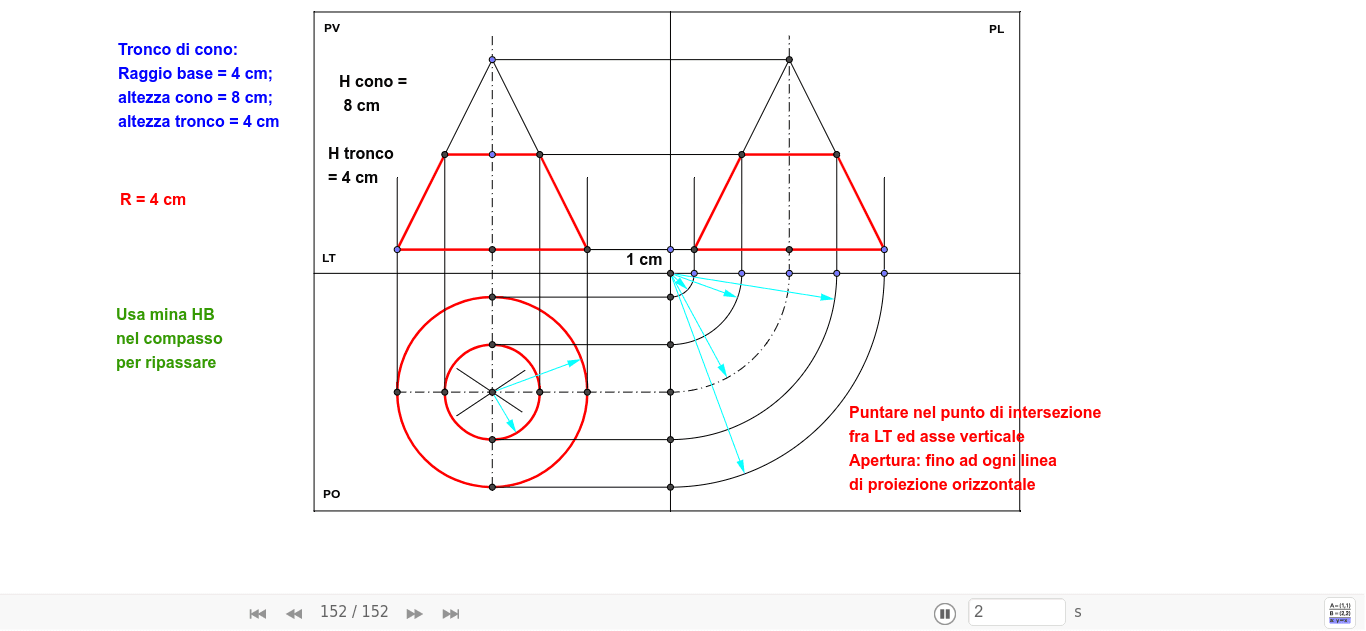
Proiezioni ortogonali Tronco di cono GeoGebra

Desarrollo tronco cono YouTube

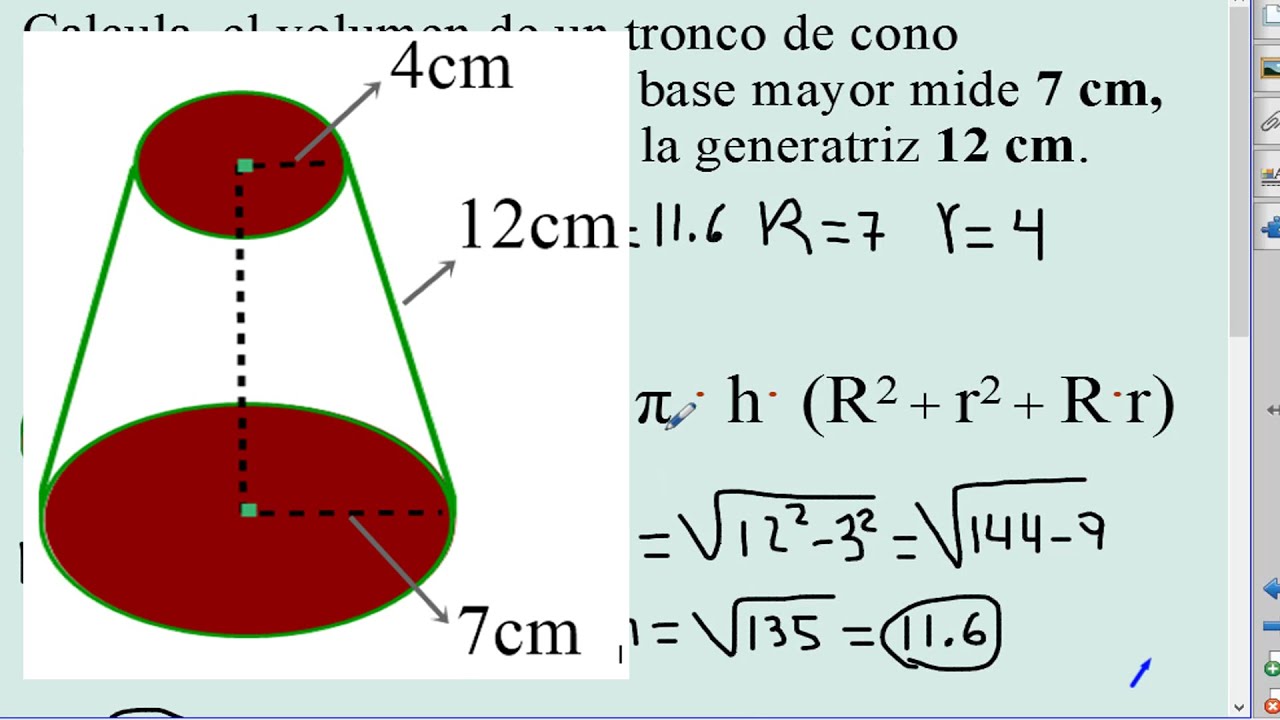
Volumen de un Tronco de Cono. YouTube

T09.4. Volumen y Área Tronco de Cono Mates 3º ESO YouTube

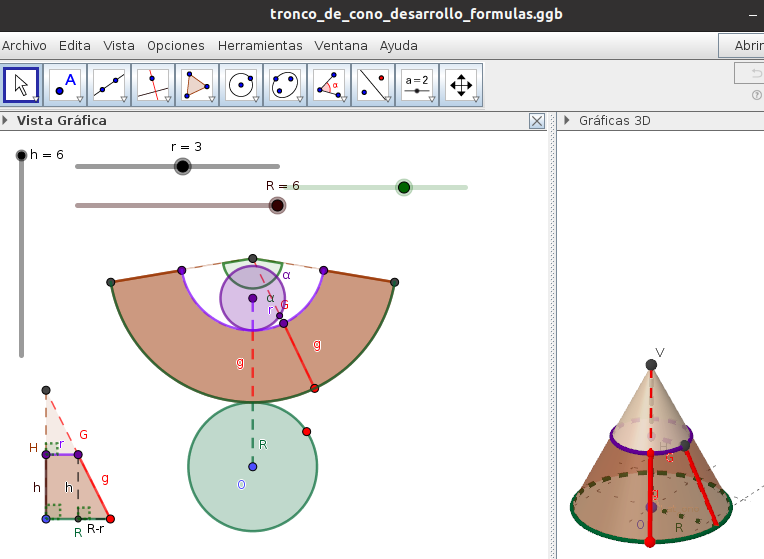
Tronco de cono desarrollo plano y fórmulas. GeoGebra

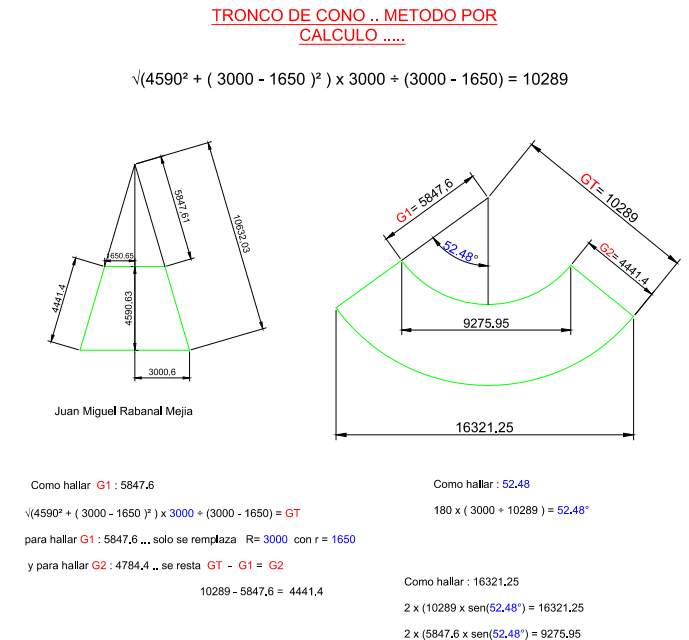
Tronco de cono metodo por calculo CALDERERIA Y SOLDARURA

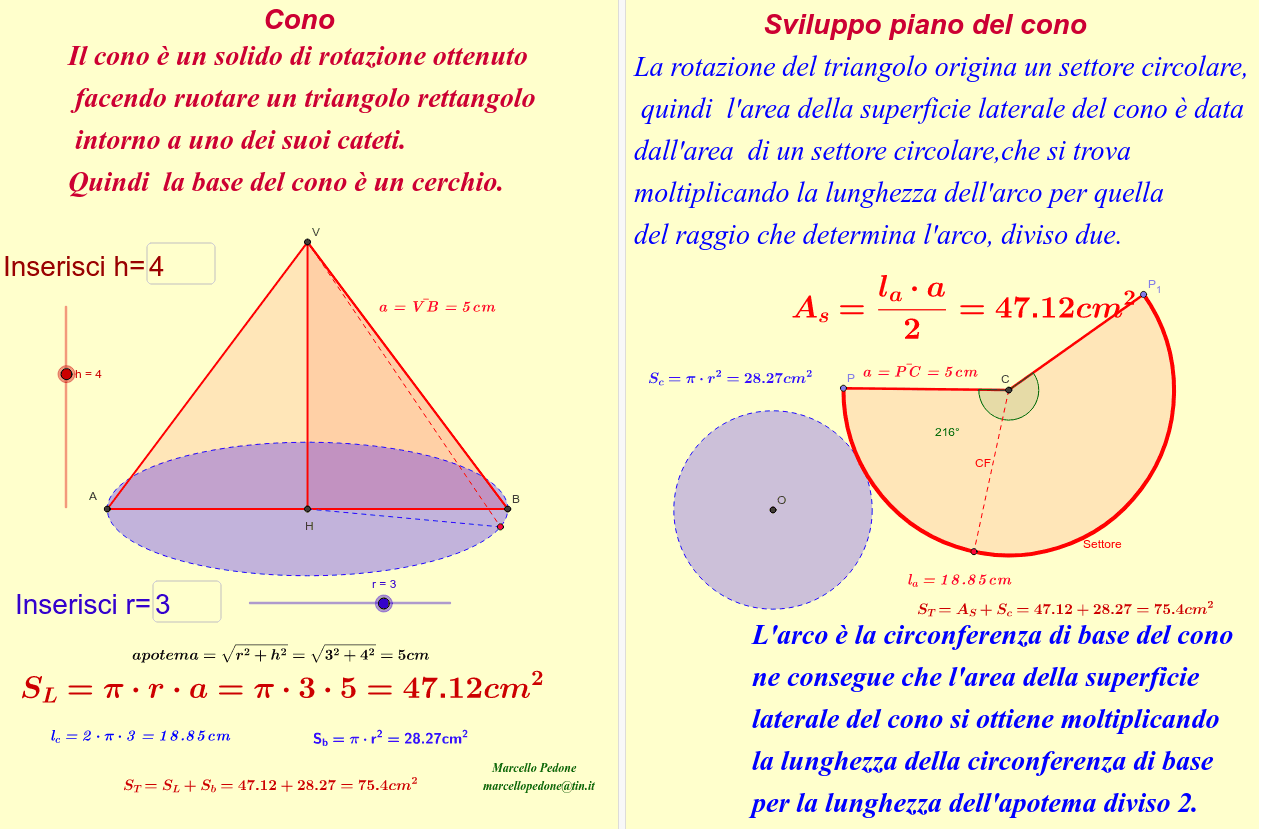
Sviluppo Piano del CONO GeoGebra

Sviluppo dei Solidi Figure Geometriche da Stampare e Costruire

Come fare un tronco di cono 7 passi

Superficie laterale del cono formule ed esempi svolti

🥇 【 Desarrollo sobre el papel de un tronco de cono de revolución Diseño y realización de

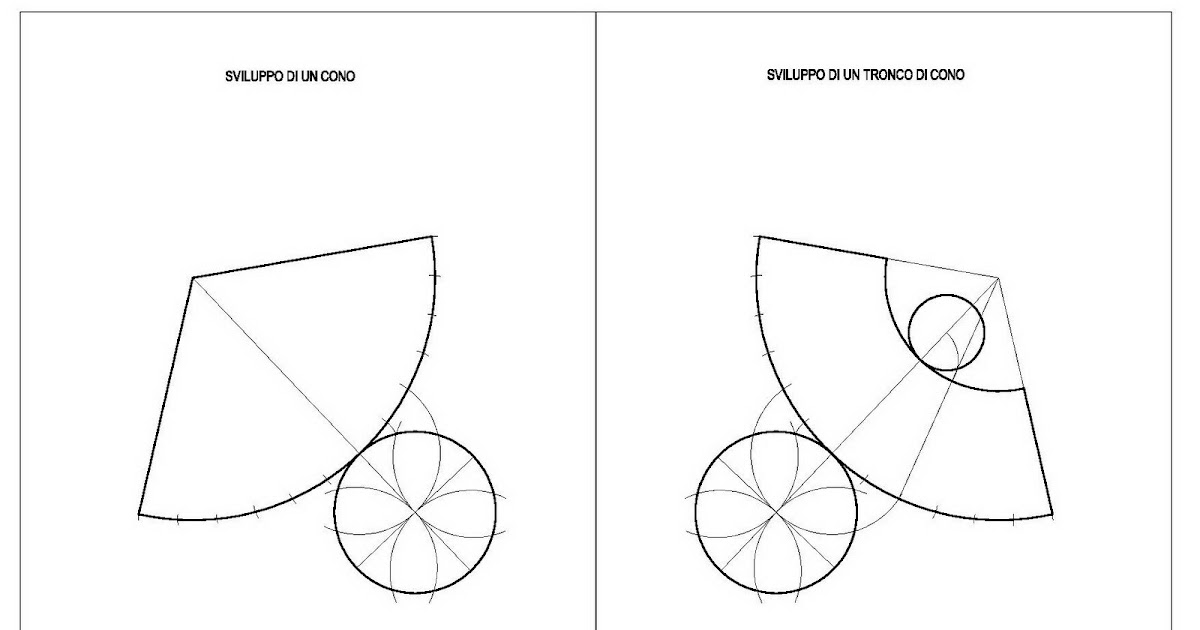
ARTEDIS 1 Classe Prima a cura del prof. Vincenzo Esposito SVILUPPO DI SOLIDI

Tutorial Solid Edge sviluppo Cono YouTube

Sviluppo piano di un cono e calcolo della sua area laterale e area totale YouTube

ÁREA Y VOLUMEN DE UN TRONCO DE CONO O CONO TRUNCADO YouTube

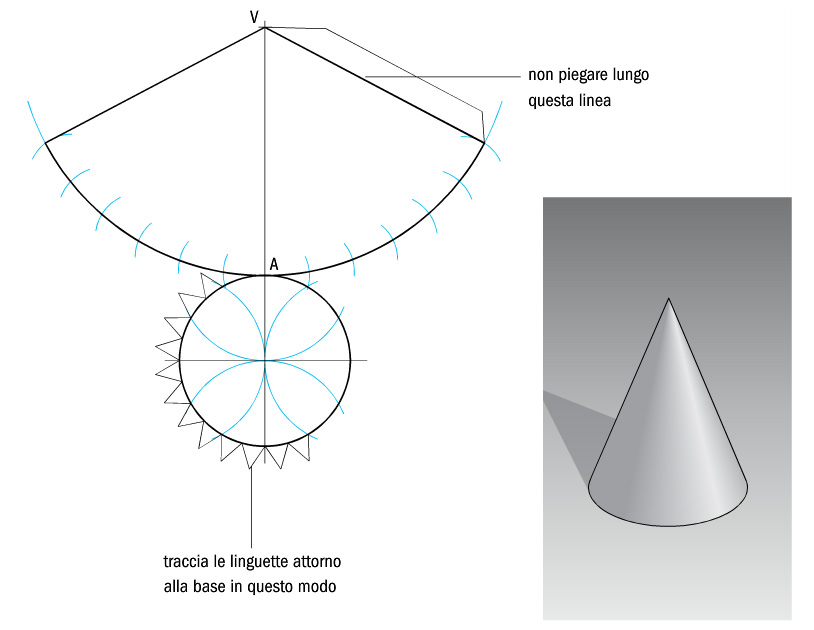
Tavole per le classi seconde A Scuola di Tecnologia

Tronco di cono definizione, formule e proprietà μatematicaΘk

Sviluppo del cono con GeoGebra YouTube

Trazado y desarrollo Tronco de cono YouTube

Assonometria isometrica di un tronco di cono YouTube

Ricaviamo la relazione che esiste tra il cerchio di base di un cono e il settore circolare che individua il suo sviluppo laterale This video was created us.. Nella geometria analitica, il cono è un tipo di superficie quadrica che può essere rappresentato attraverso un'equazione in coordinate cartesiane. Equazione generale del cono. Questa equazione generale può rappresentare diversi tipi di coni, inclusi quelli non circolari, a seconda dei valori di a, b, e c. ( x a)2 + ( y b)2 −( z c)2 = 0 ( x.